Avstand Mellan Tva Punkter – Ekonomiskt och starkt ljus för hemmet

Avstånd Mellan Två Punkter: En Komplett Guide

Introduktion till Avståndsberäkning

Att beräkna avståndet mellan två punkter är en grundläggande operation inom geometri och matematik. Det är en färdighet som är användbar i många olika områden, från navigation och kartografi till datavetenskap och fysik. I denna guide kommer vi att utforska hur man beräknar detta avstånd, de formler som används och några praktiska exempel.

Avståndsformeln i ett Tvådimensionellt Koordinatsystem

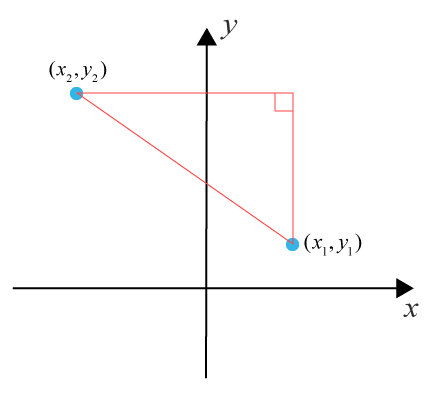
I ett tvådimensionellt koordinatsystem (x, y) kan vi beräkna avståndet mellan två punkter, P1(x1, y1) och P2(x2, y2), med hjälp av avståndsformeln. Denna formel är en direkt tillämpning av Pythagoras sats:

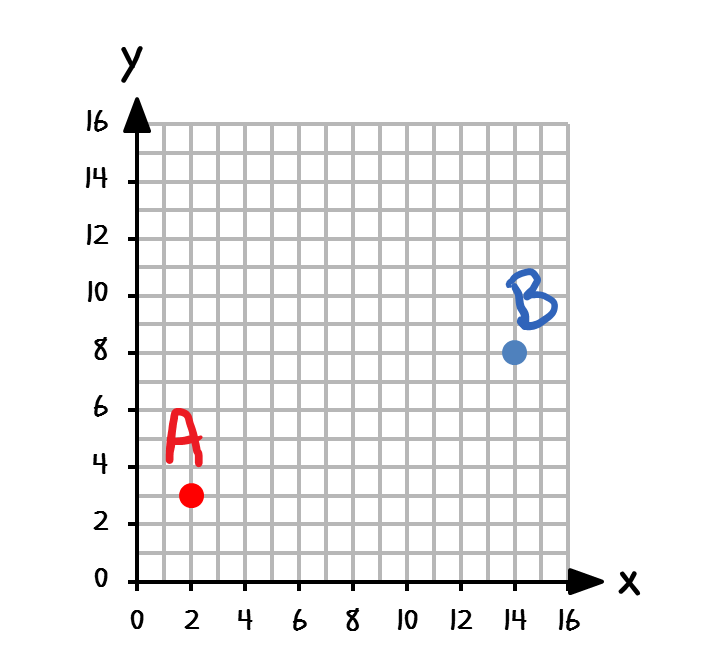
$$d = \sqrt{(x_2 – x_1)^2 + (y_2 – y_1)^2}$$

Här är ’d’ avståndet mellan punkterna. Denna formel ger oss det raka linjeavståndet mellan de två punkterna.

Exempel

Låt oss säga att vi har två punkter: P1(1, 2) och P2(4, 6). Vi kan beräkna avståndet så här:

$$d = \sqrt{(4 – 1)^2 + (6 – 2)^2} = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5$$

Så, avståndet mellan punkterna är 5 enheter.

Avståndsformeln i ett Tredimensionellt Koordinatsystem

I ett tredimensionellt koordinatsystem (x, y, z) kan vi utöka avståndsformeln för att beräkna avståndet mellan två punkter, P1(x1, y1, z1) och P2(x2, y2, z2):

$$d = \sqrt{(x_2 – x_1)^2 + (y_2 – y_1)^2 + (z_2 – z_1)^2}$$

Denna formel är en direkt utökning av den tvådimensionella formeln och ger oss det raka linjeavståndet i tre dimensioner.

Exempel

Låt oss säga att vi har två punkter: P1(1, 2, 3) och P2(4, 6, 8). Vi kan beräkna avståndet så här:

$$d = \sqrt{(4 – 1)^2 + (6 – 2)^2 + (8 – 3)^2} = \sqrt{3^2 + 4^2 + 5^2} = \sqrt{9 + 16 + 25} = \sqrt{50} \approx 7.07$$

Så, avståndet mellan punkterna är cirka 7.07 enheter.

Praktiska Tillämpningar

Avståndsberäkning används i många praktiska tillämpningar:

Navigation: GPS-system använder avståndsberäkningar för att hitta den kortaste vägen mellan två platser.

Datavetenskap: I maskininlärning används avståndsberäkningar för att bestämma likheten mellan datapunkter.

Fysik: Inom fysik används avståndsberäkningar för att analysera rörelse och krafter.

Kartografi: Kartor använder avståndsberäkningar för att bestämma avståndet mellan olika platser.

Slutsats

Att förstå och kunna beräkna avståndet mellan två punkter är en viktig färdighet inom matematik och många andra områden. Genom att använda avståndsformeln kan vi enkelt beräkna detta avstånd i både två- och tredimensionella koordinatsystem. Vi hoppas att denna guide har gett dig en tydlig förståelse för hur man utför dessa beräkningar.