RC Tidskonstant: En Fullständig Guide
Inom elektronik är RC tidskonstanten en grundläggande parameter som beskriver hur snabbt en kondensator laddas eller urladdas genom ett motstånd. Denna koncept är avgörande för att förstå och designa en mängd olika elektroniska kretsar, från enkla filter till komplexa tidskretsar. Låt oss dyka djupare in i vad RC tidskonstanten innebär och hur den används.
Vad är RC Tidskonstanten?
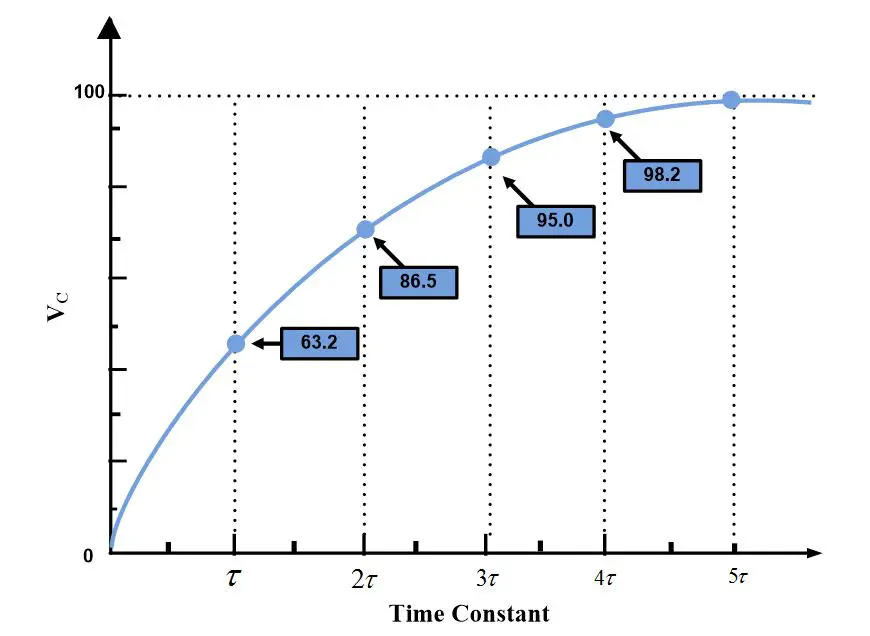
RC tidskonstanten (τ) definieras som produkten av resistansen (R) i ohm och kapacitansen (C) i farad. Den uttrycks i sekunder och representerar den tid det tar för spänningen över kondensatorn att nå cirka 63,2% av sin slutliga värde vid laddning, eller att sjunka till 36,8% av sitt initiala värde vid urladdning. Matematiskt kan detta uttryckas som:
$$ τ = R \times C $$

Denna enkla formel ger oss en kraftfull verktyg för att förutsäga och kontrollera tidssvaret hos RC-kretsar.
Beräkning av RC Tidskonstanten
För att beräkna RC tidskonstanten, behöver du bara värdena på resistansen och kapacitansen. Här är ett exempel:

Antag att vi har ett motstånd med ett värde på 10 kΩ (10 000 Ω) och en kondensator med en kapacitans på 10 μF (10 x 10-6 F). Då blir tidskonstanten:
$$ τ = 10 000 Ω \times 10 \times 10^{ -6} F = 0.1 s $$
Detta innebär att det tar 0,1 sekunder för kondensatorn att ladda till cirka 63,2% av den applicerade spänningen.
Praktiska Tillämpningar
RC tidskonstanten har en mängd olika tillämpningar inom elektronik. Här är några av de vanligaste:
- Filterkretsar: RC-kretsar används ofta som lågpass- och högpassfilter för att filtrera bort oönskade frekvenser i signaler.
- Timerkretsar: Genom att använda RC-tidskonstanten kan vi designa kretsar som genererar tidsfördröjningar eller pulser.
- Signalkonditionering: RC-kretsar används för att jämna ut signaler och minska brus.
- Oscillatorer: I vissa oscillatorer används RC-tidskonstanten för att bestämma frekvensen på den genererade signalen.
- Strömförsörjning: RC-filter används för att stabilisera och filtrera ut oönskade svängningar i strömförsörjningen.


Laddning och Urladdning
När en kondensator laddas genom ett motstånd, ökar spänningen över kondensatorn exponentiellt. Spänningen (Vc) vid tiden (t) kan beskrivas av följande formel:
$$ V_c(t) = V_0 (1 – e^{ -t/τ}) $$
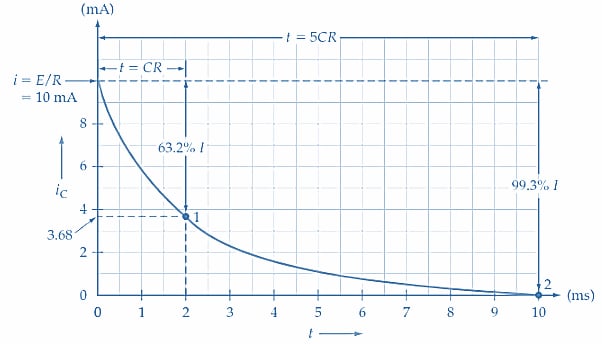
Där V0 är den applicerade spänningen. Vid urladdning minskar spänningen exponentiellt enligt:
$$ V_c(t) = V_0 e^{ -t/τ} $$
Dessa formler ger oss en exakt beskrivning av hur spänningen förändras över tiden.
Vikten av RC Tidskonstanten
Att förstå RC tidskonstanten är avgörande för att designa och analysera elektroniska kretsar. Genom att välja lämpliga värden på motstånd och kondensatorer kan vi kontrollera tidssvaret hos kretsen och uppnå önskad funktion. Det är också viktigt att notera att toleranser i komponentvärden kan påverka den faktiska tidskonstanten, vilket måste beaktas vid design.
Slutsats
RC tidskonstanten är ett fundamentalt koncept inom elektronik som ger oss verktyg för att förstå och kontrollera tidssvaret hos kretsar. Genom att behärska beräkning och tillämpningar av RC tidskonstanten kan vi designa effektiva och tillförlitliga elektroniska system. Vi hoppas att denna guide har gett dig en djupare förståelse för detta viktiga ämne.