Roten ur 2: En Fascinerande Matematisk Konstans
Roten ur 2, betecknad som √2, är ett av de mest intressanta och grundläggande talen inom matematiken. Det är ett irrationellt tal, vilket innebär att det inte kan uttryckas som en enkel bråkdel av två heltal. Detta tal har fascinerat matematiker och filosofer i århundraden, och dess betydelse sträcker sig långt bortom den teoretiska matematiken.
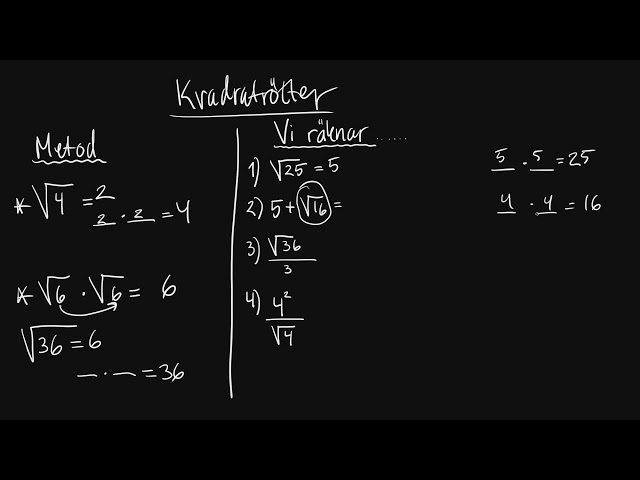
Historisk Betydelse
Redan i det antika Grekland, under Pythagoras tid, stötte man på roten ur 2. Legenden säger att Hippasus av Metapontum upptäckte att diagonalen i en kvadrat med sidan 1 var ett tal som inte kunde uttryckas som en bråkdel. Detta ledde till en kris inom den pythagoreiska skolan, som trodde att alla tal kunde uttryckas som bråkdelar. Upptäckten av roten ur 2 visade att detta inte var sant, och det var en viktig milstolpe i utvecklingen av matematiken.
Matematiska Egenskaper
Roten ur 2 är ungefär lika med 1.41421356… och fortsätter oändligt utan att upprepa sig. Detta gör det till ett transcendentalt tal. Här är några av dess intressanta egenskaper:
- Definition: √2 är det positiva tal som, när det multipliceras med sig självt, ger 2. Det vill säga, √2 * √2 = 2.
- Diagonal i en kvadrat: Som nämnts tidigare, är √2 längden på diagonalen i en kvadrat med sidan 1. Detta kan bevisas med Pythagoras sats: a² + b² = c², där a och b är sidorna och c är diagonalen. I detta fall, 1² + 1² = c², vilket ger c = √2.
- Kontinuerlig bråk: Roten ur 2 kan uttryckas som en oändlig kontinuerlig bråk: 1 + 1/(2 + 1/(2 + 1/(2 + …))).
- Trigonometri: Roten ur 2 dyker upp i trigonometriska funktioner, till exempel i värdena för sinus och cosinus för vissa vinklar.


Praktiska Tillämpningar
Även om roten ur 2 är ett abstrakt matematiskt koncept, har det flera viktiga praktiska tillämpningar:

- Konstruktion och arkitektur: I konstruktionen används √2 för att beräkna diagonaler och proportioner i byggnader.
- Kartografi: Vid kartritning används √2 för att beräkna avstånd och skalor.
- Elektronik: Inom elektronik används √2 i beräkningar relaterade till växelström och signalbehandling.
- Fotografi och design: I fotografiska och designmässiga sammanhang används förhållandet 1:√2, även känt som pappersformatet A-serien (A4, A3, etc.), för att skapa proportionella och estetiskt tilltalande format.
Bevis på Irrationellt Tal
Ett klassiskt bevis på att √2 är irrationellt använder ett motsägelsebevis. Antag att √2 är rationellt, vilket innebär att det kan uttryckas som en bråkdel a/b, där a och b är heltal utan gemensamma faktorer. Genom att kvadrera båda sidor får vi 2 = a²/b², vilket innebär att a² = 2b². Detta leder till en motsägelse, vilket bevisar att √2 inte kan vara rationellt.
Slutsats

Roten ur 2 är mycket mer än bara ett tal. Det är en matematisk konstant med djupa historiska rötter och breda praktiska tillämpningar. Dess irrationella natur utmanade tidiga matematiska antaganden och bidrog till utvecklingen av modern matematik. Genom att förstå √2 får vi en djupare inblick i matematikens skönhet och komplexitet.