cdot cdot – Ekonomiskt och starkt ljus för hemmet

Kabelarea: En Komplett Guide för Säker och Effektiv Dimensionering

Vad är kabelarea och varför är det viktigt?

Kabelarea refererar till den tvärsnittsarea av en elektrisk ledare, oftast mätt i kvadratmillimeter (mm²). Att välja rätt kabelarea är avgörande för att säkerställa en säker och effektiv elektrisk installation. En felaktig dimensionering kan leda till överbelastning, brandrisk och onödigt spänningsfall.

En för liten kabelarea kan inte hantera den ström som passerar genom den, vilket resulterar i överhettning. En för stor kabelarea är onödigt dyr och kan vara svår att installera. Därför är det viktigt att noggrant beräkna och välja rätt kabelarea baserat på installationens specifika krav.

Faktorer som påverkar kabelarea

Strömstyrka (Ampere): Den maximala strömmen som kabeln ska hantera.
Spänningsfall: Den minskning av spänning som uppstår över kabelns längd.
Kabellängd: Längre kablar kräver större kabelarea för att minimera spänningsfallet.
Installationstyp: Hur kabeln installeras påverkar dess värmeavledning och därmed dess strömhanteringskapacitet.
Omgivningstemperatur: Högre temperaturer minskar kabelns strömhanteringskapacitet.
Ledarmaterial: Koppar och aluminium har olika ledningsförmåga, vilket påverkar den nödvändiga kabelarean.

Hur man beräknar kabelarea

För att beräkna rätt kabelarea behöver du ta hänsyn till ovanstående faktorer. Det finns olika tabeller och formler som kan användas, men det är alltid bäst att rådgöra med en behörig elektriker.

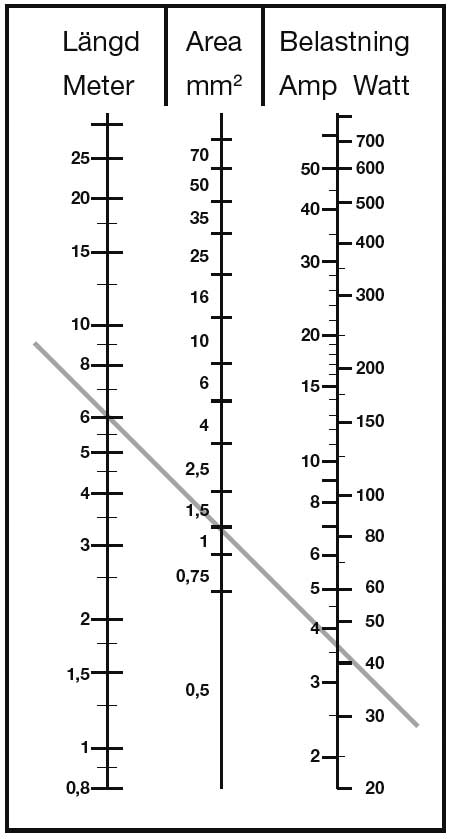
En vanlig metod är att använda formeln för spänningsfall: $$ \Delta U = \frac{2 \cdot L \cdot I \cdot \rho}{A} $$ där:

$\Delta U$ är spänningsfallet (volt)
$L$ är kabellängden (meter)
$I$ är strömstyrkan (ampere)
$\rho$ är resistiviteten för ledarmaterialet (ohm·mm²/meter)

$A$ är kabelarean (mm²)

Genom att lösa formeln för $A$ kan du beräkna den minsta nödvändiga kabelarean för att hålla spänningsfallet inom acceptabla gränser.

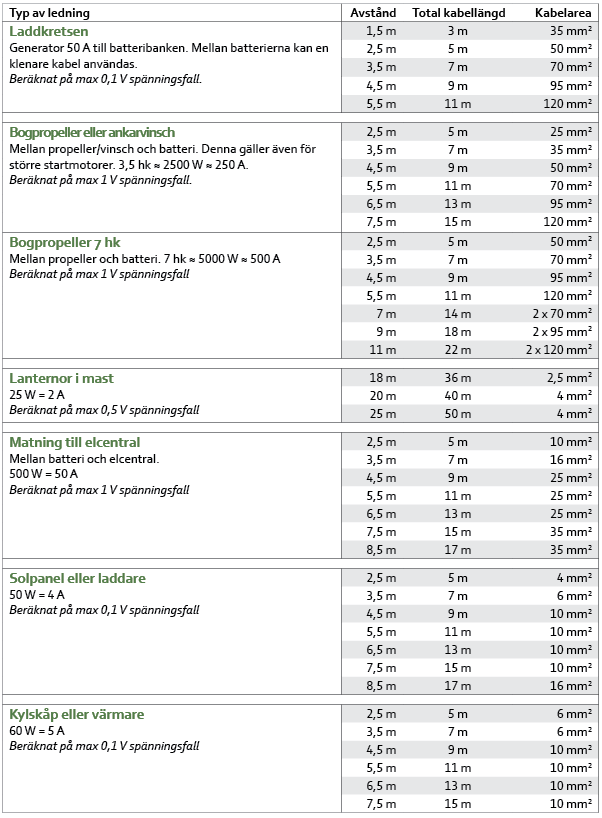
Vanliga kabelarea och deras användningsområden

1,5 mm²: Belysning och mindre apparater.
2,5 mm²: Vanliga eluttag och kraftuttag.
4 mm²: Spisar, ugnar och andra större apparater.
6 mm²: Större kraftuttag och långa kabeldragningar.
10 mm² och större: Industriella installationer och huvudledningar.

Säkerhet och standarder

Det är viktigt att följa gällande säkerhetsstandarder och föreskrifter när du väljer och installerar elektriska kablar. Använd alltid kablar som är godkända enligt relevanta standarder, såsom SS 424 14 24.

Rådgör alltid med en behörig elektriker för att säkerställa att din installation är säker och korrekt utförd.

Materialval: Koppar eller Aluminium?

Både koppar och aluminium används som ledarmaterial i elektriska kablar. Koppar har högre ledningsförmåga, men aluminium är lättare och billigare.

Vid val av material är det viktigt att ta hänsyn till installationens specifika krav och kostnadsaspekter.

Sammanfattning

Att förstå och korrekt dimensionera kabelarea är avgörande för en säker och effektiv elektrisk installation. Genom att ta hänsyn till strömstyrka, spänningsfall, kabellängd och andra relevanta faktorer kan du välja rätt kabel för din applikation.

Kom ihåg att alltid rådgöra med en behörig elektriker för att säkerställa att din installation är säker och uppfyller alla gällande standarder.

Boolesk Algebra: En Djupgående Förklaring

Boolesk algebra är en gren av matematiken som handlar om logiska operationer. Istället för att räkna med siffror, räknar vi med sanningar och falskheter, representerade av 1 och 0. Denna algebra är grundläggande för datavetenskap och digital elektronik, eftersom den ger oss verktygen att analysera och designa logiska kretsar.

Grundläggande Operationer

I boolesk algebra arbetar vi med tre grundläggande operationer:

OCH (AND): Representeras av symbolen $\cdot$ eller $\land$. Resultatet är 1 (sant) endast om båda ingångarna är 1.
ELLER (OR): Representeras av symbolen $+$ eller $\lor$. Resultatet är 1 (sant) om minst en av ingångarna är 1.

ICKE (NOT): Representeras av symbolen $\neg$ eller en överstrykning. Resultatet är motsatsen till ingången. Om ingången är 1, är resultatet 0, och vice versa.

Sanningstabeller

För att bättre förstå dessa operationer använder vi sanningstabeller. Här är några exempel:

OCH (AND)

ABA $\cdot$ B

0	0	0
0	1	0
1	0	0
1	1	1

ELLER (OR)

ABA + B

0	0	0
0	1	1
1	0	1
1	1	1

ICKE (NOT)

A$\neg$A

0	1
1	0

Tillämpningar av Boolesk Algebra

Boolesk algebra används i en mängd olika områden, inklusive:

Digital elektronik: För att designa logiska kretsar i datorer och andra digitala enheter.
Datavetenskap: För att optimera databasfrågor och sökalgoritmer.
Programmering: För att skapa villkorssatser och logiska uttryck.
Nätverksteknik: För att hantera nätverksåtkomst och säkerhet.

Artificiell intelligens: För att utveckla logiska system och expertdatorsystem.

Booleska Uttryck och Förenkling

Vi kan kombinera booleska operationer för att skapa komplexa uttryck. Till exempel: $(A \cdot B) + \neg C$. En viktig del av boolesk algebra är att förenkla dessa uttryck för att göra dem mer effektiva. Detta kan göras med hjälp av olika lagar och regler, som De Morgans lagar och distributiva lagen.

De Morgans lagar:

$\neg (A \cdot B) = \neg A + \neg B$
$\neg (A + B) = \neg A \cdot \neg B$

Distributiva lagen:

$A \cdot (B + C) = (A \cdot B) + (A \cdot C)$
$A + (B \cdot C) = (A + B) \cdot (A + C)$

Varför Är Boolesk Algebra Viktigt?

Boolesk algebra är en hörnsten inom digital teknik. Utan den skulle vi inte kunna bygga datorer, smartphones eller andra digitala enheter som vi använder varje dag. Genom att förstå boolesk algebra kan vi bättre förstå hur dessa enheter fungerar och hur vi kan använda dem för att lösa komplexa problem.

Genom att behärska grunderna i boolesk algebra, kan du skapa kraftfulla system och lösningar. Det är ett grundläggande verktyg för alla som är intresserade av datavetenskap, digital elektronik eller programmering.

För att fortsätta din resa i boolesk algebra, rekommenderar vi att du utforskar olika online-resurser, övar på att lösa logiska problem och experimenterar med digitala kretsar. Kom ihåg att övning ger färdighet!