kraften appliceras – Ekonomiskt och starkt ljus för hemmet

Kraftmoment Formel: En Djupgående Förklaring

Vad är Kraftmoment?

Inom fysiken är kraftmoment, även kallat vridmoment, ett mått på en krafts förmåga att få ett objekt att rotera runt en axel. Det är en central koncept inom mekaniken och har tillämpningar inom en rad olika områden, från ingenjörskonst till vardagliga situationer.

Tänk dig att du försöker öppna en dörr. Ju längre bort från gångjärnen du trycker, desto lättare är det att öppna dörren. Detta beror på att kraftmomentet ökar med avståndet från rotationsaxeln.

Kraftmoment Formel: En Detaljerad Genomgång

Den grundläggande kraftmoment formeln är:

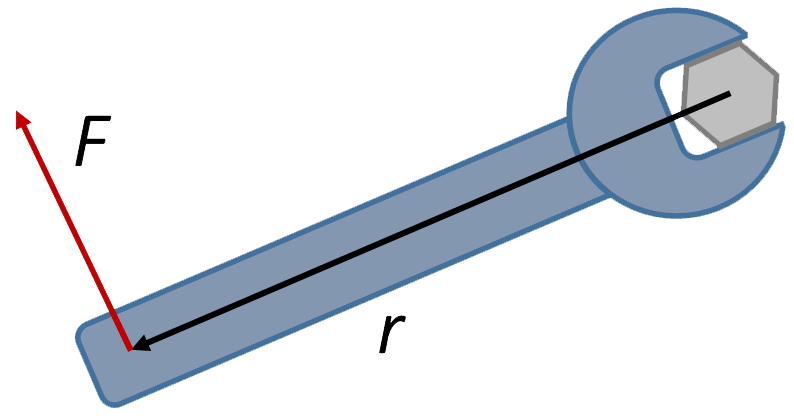
τ = r × F × sin(θ)

Där:

τ (tau) är kraftmomentet, mätt i Newtonmeter (Nm).

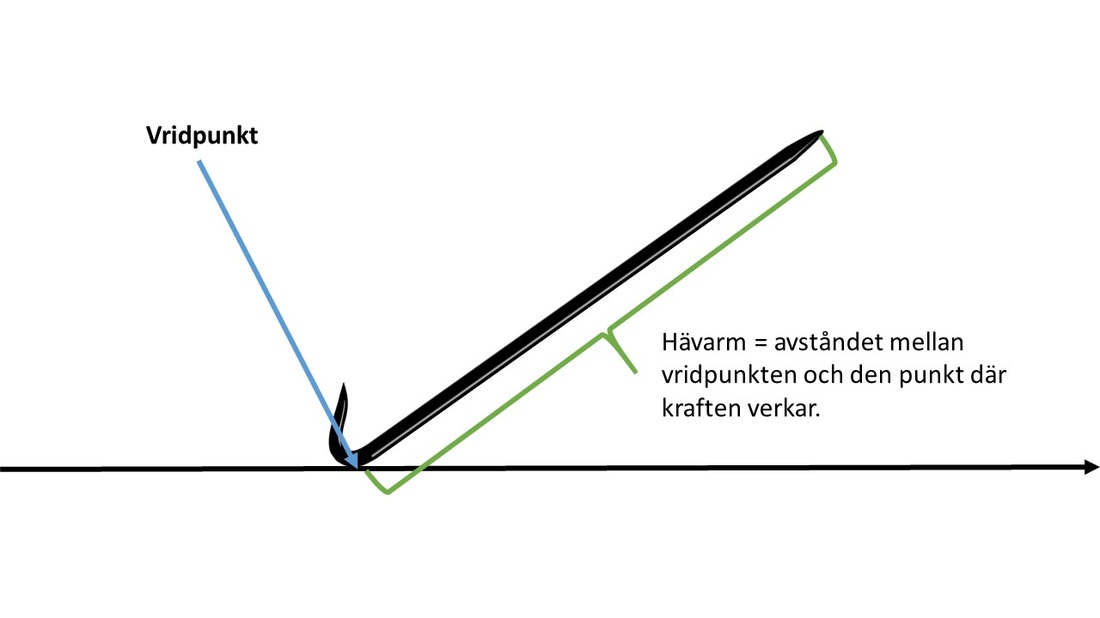
r är avståndet från rotationsaxeln till den punkt där kraften appliceras, mätt i meter (m).

F är den applicerade kraften, mätt i Newton (N).

θ (theta) är vinkeln mellan kraftvektorn och avståndsvektorn.

Om kraften appliceras vinkelrätt mot avståndsvektorn (θ = 90°), förenklas formeln till:

τ = r × F

Praktiska Exempel på Kraftmoment

Här är några exempel på hur kraftmoment formeln används i praktiken:

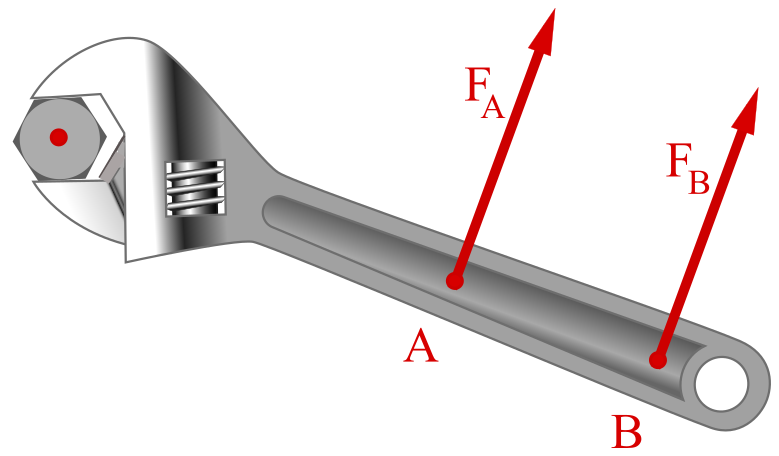
Att öppna en skiftnyckel: När du använder en skiftnyckel för att dra åt en mutter, applicerar du ett kraftmoment. Ju längre skiftnyckeln är, desto större kraftmoment kan du generera.

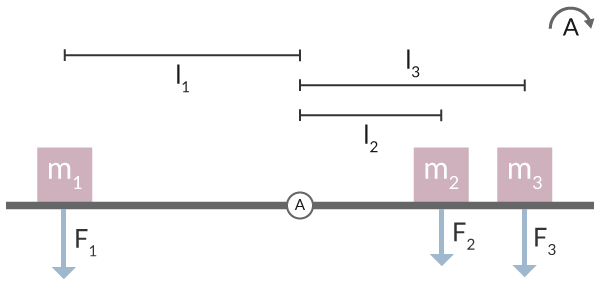
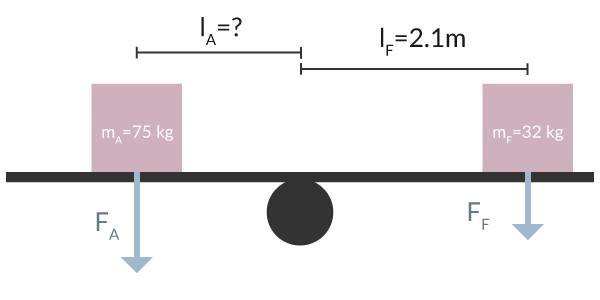
Balans på en gungbräda: För att balansera en gungbräda måste kraftmomenten på båda sidor vara lika stora.

Motorns vridmoment: I en bilmotor genererar vridmomentet den kraft som driver hjulen.

Dörröppning: Som nämnt tidigare, dörröppning är ett bra exempel, där avståndet från gångjärnen och kraften som appliceras avgör hur lätt dörren öppnas.

Vikten av Vinkeln i Kraftmoment Formeln

Vinkeln, representerad som θ i formeln, är kritisk. Om kraften appliceras parallellt med avståndsvektorn (θ = 0° eller 180°), är sin(θ) = 0, och därmed blir kraftmomentet noll. Detta innebär att en kraft som verkar direkt längs avståndsvektorn inte skapar någon rotation.

Tillämpningar inom Ingenjörskonst

Inom ingenjörskonsten är förståelsen av kraftmoment avgörande för att designa och analysera roterande system. Det används vid:

Design av motorer och transmissioner.

Analys av strukturer som broar och byggnader.

Utveckling av robotar och andra mekaniska system.

Sammanfattning

Kraftmoment formeln är ett grundläggande verktyg inom fysiken och ingenjörskonsten. Genom att förstå hur man beräknar kraftmoment kan vi analysera och designa en mängd olika roterande system. Kom ihåg att både kraftens storlek och avståndet från rotationsaxeln spelar en avgörande roll.

För att bemästra denna formel, öva med olika problem och tillämpningar. Genom att göra det kommer du att få en djupare förståelse för hur rotation fungerar i vår värld.

Räkna ut Vridmoment: En Komplett Guide

Vridmoment, eller moment som det ibland kallas, är en fundamental storhet inom mekanik och fysik. Det beskriver den roterande kraften som appliceras på ett objekt. Att förstå hur man räknar ut vridmoment är avgörande inom många områden, från ingenjörskonst till vardagliga mekaniska tillämpningar. Denna guide ger dig en djupgående förståelse för vridmoment och hur du beräknar det.

Vad är Vridmoment?

Vridmoment är den kraft som får ett objekt att rotera runt en axel. Det är inte bara kraften i sig, utan även avståndet från rotationsaxeln där kraften appliceras. Tänk dig att du försöker öppna en dörr. Om du trycker nära gångjärnen krävs det mycket mer kraft än om du trycker längst ut på handtaget. Detta beror på att avståndet från rotationsaxeln (gångjärnen) påverkar vridmomentet.

Formeln för Vridmoment

Den grundläggande formeln för att räkna ut vridmoment är:

$$ \tau = r \times F \times \sin(\theta) $$

Där:

$\tau$ (tau) är vridmomentet (mäts i Newtonmeter, Nm).
$r$ är avståndet från rotationsaxeln till punkten där kraften appliceras (mäts i meter, m).

$F$ är kraften som appliceras (mäts i Newton, N).
$\theta$ (theta) är vinkeln mellan kraftvektorn och avståndsvektorn.

I många praktiska tillämpningar är vinkeln $\theta$ 90 grader, vilket innebär att $\sin(90^\circ) = 1$. Då förenklas formeln till:

$$ \tau = r \times F $$

Exempel på Beräkning av Vridmoment

Låt oss ta ett exempel för att illustrera hur man räknar ut vridmoment:

Anta att du använder en skiftnyckel för att dra åt en bult. Skiftnyckeln är 0.25 meter lång, och du applicerar en kraft på 50 Newton i en vinkel på 90 grader.

Använder vi den förenklade formeln:

$$ \tau = 0.25 \text{ m} \times 50 \text{ N} = 12.5 \text{ Nm} $$

Vridmomentet som appliceras på bulten är 12.5 Newtonmeter.

Praktiska Tillämpningar av Vridmoment

Vridmoment är en viktig faktor inom många områden:

Bilindustri: För att designa motorer, växellådor och bromssystem.
Byggindustri: För att beräkna krafter i konstruktioner och maskiner.
Flygindustri: För att designa flygplansmotorer och styrsystem.
Robotik: För att styra robotarmars rörelser och kraft.
Sport: För att analysera och optimera rörelser inom olika sporter.

Viktiga Faktorer att Tänka På

När du räknar ut vridmoment, är det viktigt att tänka på:

Enheter: Se till att alla enheter är konsistenta (meter, Newton, radianer).
Vinkel: Vinkeln mellan kraften och avståndet påverkar vridmomentet avsevärt.
Rotationsaxel: Vridmomentet beror på var rotationsaxeln är placerad.
Kraftens riktning: Kraftens riktning avgör rotationsriktningen.

Tabell över Vanliga Vridmoment Enheter

Enhet

Beskrivning

Newtonmeter (Nm)	Standardenhet för vridmoment.
Pundfot (lb-ft)	Vanligt i USA och Storbritannien.
Kilogrammeter (kg-m)	Används ibland i tekniska sammanhang.

Slutsats

Att räkna ut vridmoment är en viktig färdighet inom många tekniska och vetenskapliga områden. Genom att förstå formeln och dess tillämpningar kan du analysera och designa system som involverar rotation. Kom ihåg att alltid vara noggrann med enheter och vinklar för att få korrekta resultat. Genom att bemästra detta koncept kan du öppna upp en värld av möjligheter inom mekanik och fysik.