PID-regulator C-kod: En djupgående guide
Introduktion till PID-regulatorer
En PID-regulator (Proportionell-Integrerande-Deriverande) är en av de mest använda styrteknikerna inom industriell automation och inbyggda system. Dess förmåga att noggrant kontrollera processer gör den oumbärlig i en mängd olika applikationer, från temperaturkontroll till robotstyrning. Denna artikel ger en detaljerad genomgång av hur du implementerar en PID-regulator i C-kod, med fokus på både teori och praktiska exempel.
Grundläggande PID-teori
En PID-regulator består av tre delar:

- Proportionell (P): Den proportionella termen ger en utsignal som är proportionell mot felet mellan önskat värde (setpoint) och aktuellt värde (processvärde).
- Integrerande (I): Den integrerande termen eliminerar kvarstående fel (steady-state error) genom att summera tidigare fel.
- Deriverande (D): Den deriverande termen förutser framtida fel genom att analysera förändringstakten av felet, vilket förbättrar systemets respons.
Den matematiska representationen av en PID-regulator är:
$$u(t) = K_p e(t) + K_i \int_0^t e(\tau) d\tau + K_d \frac{de(t)}{dt}$$

Där:
- $u(t)$ är utsignalen från regulatorn.
- $e(t)$ är felet (setpoint – processvärde).
- $K_p$, $K_i$, och $K_d$ är de proportionella, integrerande och deriverande förstärkningskonstanterna.
Implementering av PID i C-kod
Att implementera en PID-regulator i C-kod kräver noggrannhet och förståelse för de diskreta tidsstegen som används i digitala system. Här är ett grundläggande exempel:
float kp, ki, kd; // PID-konstanter float setpoint, processValue; // Önskat och aktuellt värde float integral, previousError; // Integralt och tidigare fel
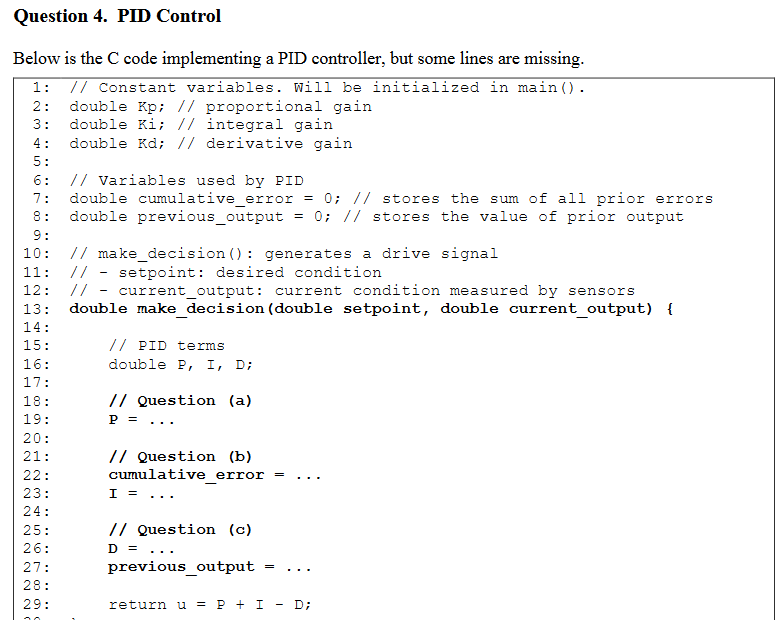
float calculatePID(float dt) { float error = setpoint – processValue; integral += error * dt; float derivative = (error – previousError) / dt; float output = kp * error + ki * integral + kd * derivative; previousError = error; return output; }

I detta exempel representerar `dt` tidssteget mellan beräkningarna. Det är viktigt att välja lämpliga värden för `kp`, `ki` och `kd` för att uppnå önskad prestanda. Detta kallas för PID-tuning.
PID-tuning och optimering
PID-tuning är processen att justera konstanterna `kp`, `ki` och `kd` för att optimera systemets respons. Vanliga metoder inkluderar Ziegler-Nichols och Cohen-Coon. Det är viktigt att förstå att olika applikationer kräver olika tuningstrategier.

För att optimera din C-kod för PID-reglering, överväg följande:
- Tidssteg (dt): Välj ett lämpligt tidssteg baserat på systemets dynamik.
- Anti-windup: Implementera anti-windup för att förhindra att integralt termen blir för stor vid mättnad.
- Filtrering av derivata: Använd ett lågpassfilter för att minska brus i derivata termen.
- Diskretisering: Använd lämpliga diskretiseringsmetoder (t.ex. Euler-metoden eller Tustin-metoden) för att omvandla den kontinuerliga PID-regulatorn till en diskret form.
Praktiska tillämpningar
PID-regulatorer används i en mängd olika tillämpningar, inklusive:
- Temperaturkontroll: I ugnar, kylsystem och klimatanläggningar.
- Hastighetskontroll: För motorer och robotar.
- Tryckkontroll: I industriella processer.
- Flödeskontroll: Inom kemisk industri och vattenrening.

Genom att implementera en effektiv PID-regulator i C-kod kan du uppnå hög precision och stabilitet i dessa system.
Slutsats
Att förstå och implementera PID-regulatorer i C-kod är en viktig färdighet för ingenjörer inom automation och inbyggda system. Genom att behärska teorin och praktiken bakom PID-reglering kan du skapa robusta och effektiva styrsystem för en mängd olika applikationer. Genom noggrann PID-tuning och optimering av din C-kod kan du maximera prestandan och tillförlitligheten hos dina system.