resistorerna kopplade

Ersättningsresistans: Förståelse och Tillämpningar

Vad är Ersättningsresistans?

I elektriska kretsar, särskilt de som innehåller flera resistorer, är det ofta nödvändigt att beräkna den totala resistansen. Denna totala resistans kallas för ersättningsresistans. Det är den enkla resistans som skulle ge samma totala ström och spänningsförhållande som den komplexa kombinationen av resistorer.

Att förstå ersättningsresistansens beräkning är avgörande för att analysera och designa elektriska kretsar effektivt. Den hjälper oss att förenkla komplexa kretsar och förutsäga deras beteende.

Beräkning av Ersättningsresistans

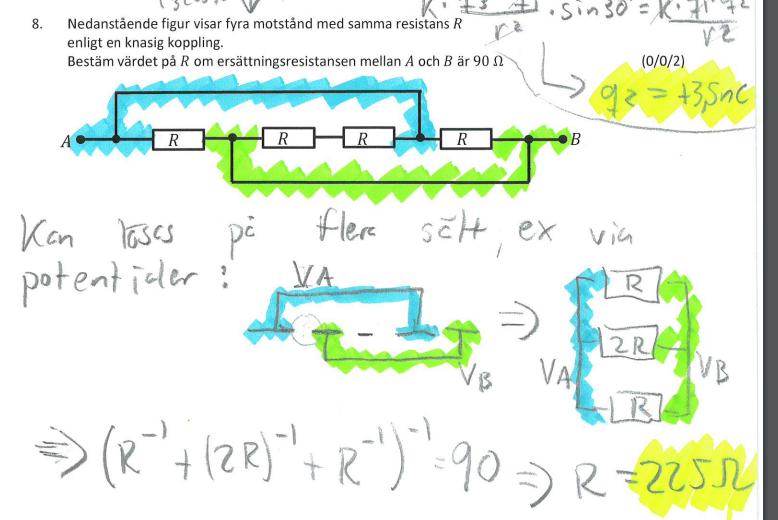
Beräkningen av ersättningsresistans varierar beroende på hur resistorerna är kopplade. Det finns två grundläggande kopplingstyper: seriekoppling och parallellkoppling.

Seriekoppling

I en seriekoppling är resistorerna kopplade efter varandra, så att strömmen måste passera genom varje resistor i följd. För att beräkna ersättningsresistansen i en seriekoppling adderar vi helt enkelt resistansvärdena för varje resistor:

$$R_{tot} = R_1 + R_2 + R_3 + … + R_n$$

Här är $R_{tot}$ ersättningsresistansen, och $R_1, R_2, R_3, …, R_n$ är resistansvärdena för de enskilda resistorerna.

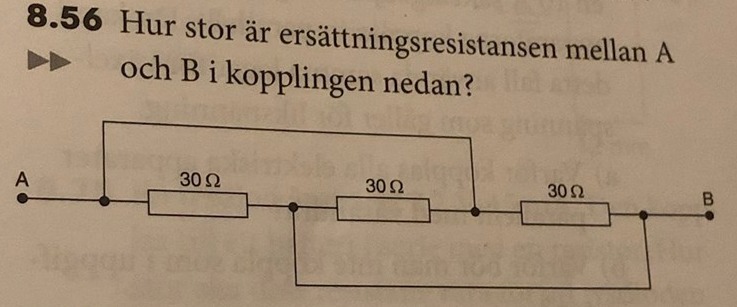
Parallellkoppling

I en parallellkoppling är resistorerna kopplade så att strömmen kan ta flera vägar. För att beräkna ersättningsresistansen i en parallellkoppling använder vi följande formel:

$$\frac{1}{R_{tot}} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} + … + \frac{1}{R_n}$$

Efter att ha beräknat summan av de inverterade resistansvärdena, tar vi det inverterade värdet av summan för att få $R_{tot}$, ersättningsresistansen.

Praktiska Tillämpningar

Ersättningsresistans är ett grundläggande koncept inom elektronik och har många praktiska tillämpningar. Här är några exempel:

Kretsdesign: Ingenjörer använder ersättningsresistans för att förenkla komplexa kretsar och beräkna ström- och spänningsförhållanden.

Felsökning: Genom att mäta ersättningsresistansen kan tekniker identifiera fel i elektriska system.

Sensorer: Många sensorer använder resistiva element vars resistans ändras med fysiska parametrar. Genom att beräkna ersättningsresistansen kan vi mäta dessa parametrar.

Ljudsystem: I ljudsystem används ersättningsresistans för att matcha impedanser och optimera signalöverföringen.

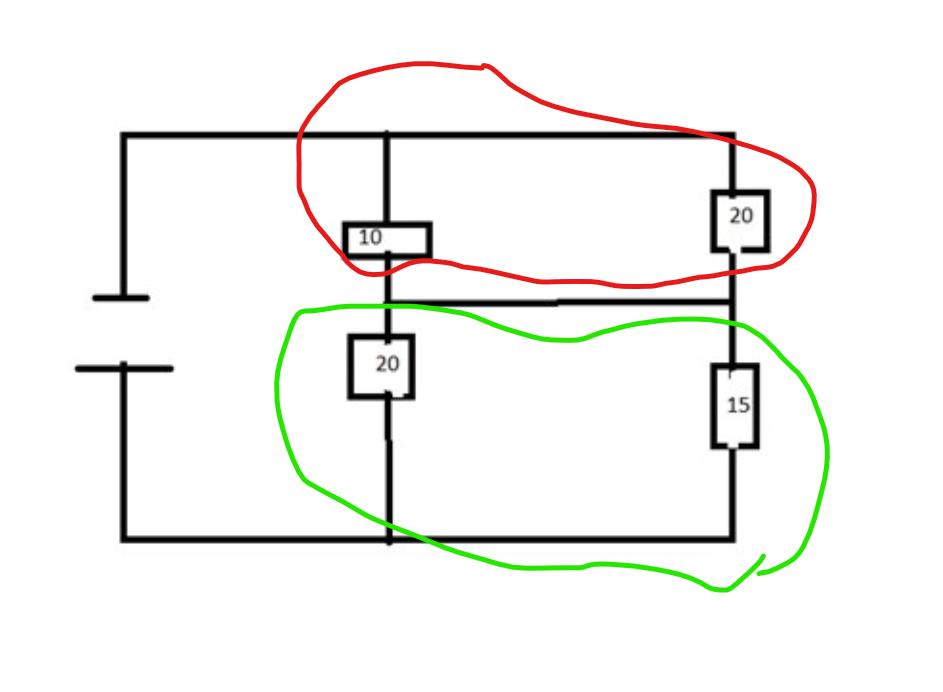
Viktiga Begrepp och Tips

För att bemästra beräkningen av ersättningsresistans, är det viktigt att förstå följande begrepp:

Ohms lag: Relationen mellan spänning, ström och resistans ($V = IR$).

Kirchhoffs lagar: Lagarna för ström och spänning i elektriska kretsar.

Resistorers tolerans: De variationer i resistansvärden som kan förekomma hos resistorer.

När du beräknar ersättningsresistans, se till att:

Identifiera om resistorerna är kopplade i serie eller parallellt.

Använd rätt formel för varje kopplingstyp.

Dubbelkolla dina beräkningar för att undvika fel.

Slutsats

Ersättningsresistans är ett grundläggande och viktigt koncept inom elektronik. Genom att förstå hur man beräknar och tillämpar ersättningsresistans, kan vi analysera och designa elektriska kretsar mer effektivt. Denna kunskap är ovärderlig för både studenter och professionella inom elektronikområdet.