Sann Sann – Ekonomiskt och starkt ljus för hemmet

Sanningstabell Logik: En Djupdykning i Logikens Värld

Logik är grunden för resonemang och argumentation. Inom logiken används sanningstabeller för att systematiskt analysera och förstå hur logiska utsagor hänger ihop. Denna artikel utforskar djupgående konceptet sanningstabell logik, dess tillämpningar och betydelse inom olika discipliner.

Vad är en Sanningstabell?

En sanningstabell är ett matematiskt verktyg som används inom satslogik och boolesk algebra. Den visar alla möjliga kombinationer av sanningsvärden för logiska utsagor och resultatet av logiska operationer på dessa utsagor. I grunden är det en tabell som visar om en logisk utsaga är sann eller falsk under olika omständigheter.

Logiska Operatorer

För att skapa sanningstabeller använder vi olika logiska operatorer. De mest grundläggande är:

OCH (konjunktion, $\land$): Båda utsagor måste vara sanna för att resultatet ska vara sant.
ELLER (disjunktion, $\lor$): Minst en av utsagorna måste vara sann för att resultatet ska vara sant.
INTE (negation, $\neg$): Vänder på sanningsvärdet. Om utsagan är sann, blir resultatet falskt, och vice versa.
IMPLIKATION (om…så…, $\rightarrow$): Resultatet är falskt endast om den första utsagan är sann och den andra är falsk.
EKVIVALENS (om och endast om, $\leftrightarrow$): Resultatet är sant om båda utsagorna har samma sanningsvärde.

Hur man Skapar en Sanningstabell

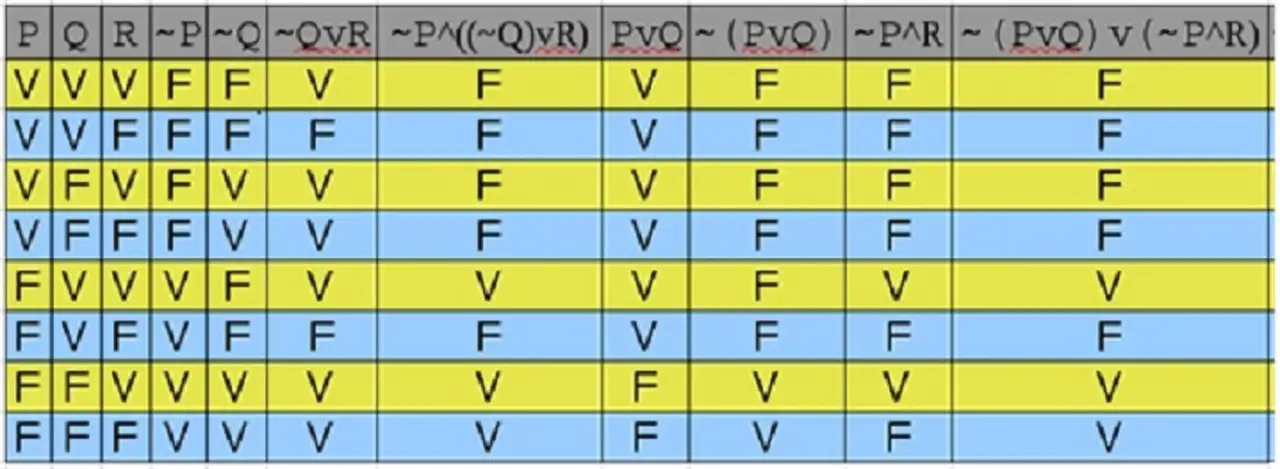
Låt oss ta ett exempel med två utsagor, P och Q, och undersöka OCH-operatorn (P $\land$ Q):

P $\land$ Q

Sann	Sann	Sann
Sann	Falsk	Falsk
Falsk	Sann	Falsk
Falsk	Falsk	Falsk

Samma princip tillämpas för andra logiska operatorer. Tabellerna blir större ju fler utsagor som ingår.

Betydelsen av Sanningstabeller

Sanningstabeller är viktiga inom flera områden:

Matematik: De används för att bevisa matematiska satser och logiska samband.
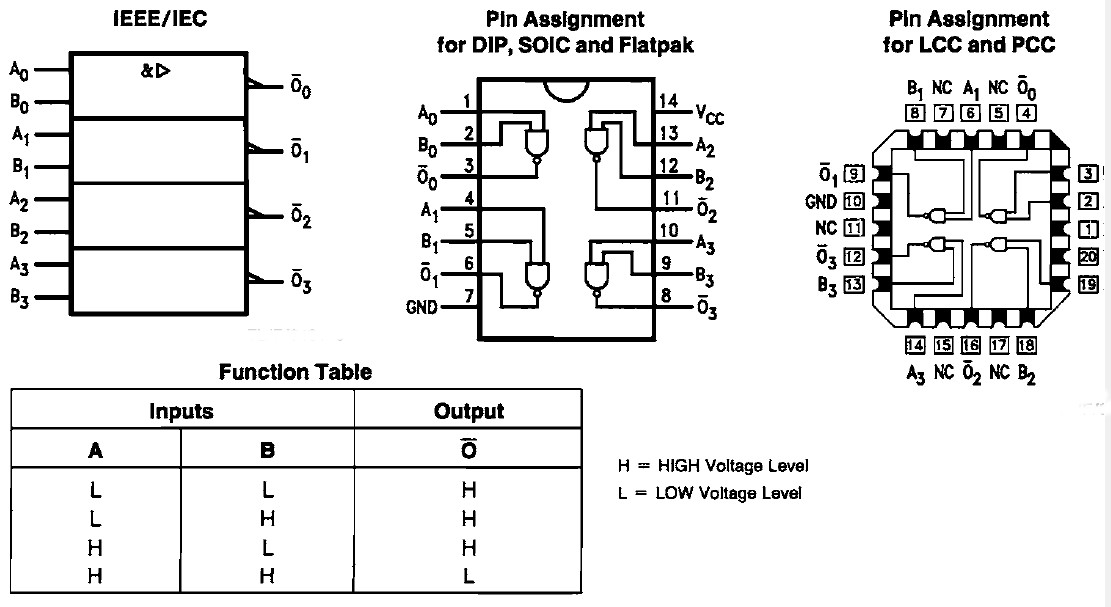
Datavetenskap: Inom digital elektronik och programmering används de för att designa logiska kretsar och algoritmer.
Filosofi: De hjälper till att analysera argument och bedöma deras giltighet.

Tillämpningar i Datavetenskap

Inom datavetenskap är sanningstabeller grundläggande för att förstå hur datorer fungerar på en grundläggande nivå. Logiska grindar, som används i processorer och minneskretsar, bygger på boolesk logik och kan beskrivas med hjälp av sanningstabeller. Detta gör att vi kan designa komplexa system som utför beräkningar och hanterar data.

Filosofiska Implikationer

Inom filosofin används sanningstabeller för att analysera argument och bedöma deras giltighet. Genom att bryta ner argument i logiska utsagor och använda sanningstabeller kan vi avgöra om ett argument är logiskt giltigt eller inte. Detta är avgörande för att säkerställa att våra resonemang är korrekta och välgrundade.

Slutsats

Sanningstabell logik är ett kraftfullt verktyg för att analysera och förstå logiska samband. Genom att behärska sanningstabeller kan man få en djupare insikt i logikens principer och deras tillämpningar inom matematik, datavetenskap och filosofi. Oavsett om du är student, forskare eller bara intresserad av logik, är sanningstabeller en ovärderlig resurs.

Och Eller Icke Logik: En Djupdykning i Logiska Operationer

Introduktion till Logiska Operationer

Logik är grundläggande för hur vi tänker, resonerar och löser problem. I hjärtat av logiken finns tre grundläggande operationer: OCH, ELLER, och ICKE. Dessa operationer, som ofta kallas booleska operationer, är avgörande inom områden som matematik, datavetenskap och digitalteknik. Denna artikel kommer att utforska dessa operationer i detalj, förklara deras funktion och visa hur de tillämpas i olika sammanhang.

OCH (Konjunktion)

OCH-operationen, eller konjunktion, är sann endast om båda ingående påståenden är sanna. I vardagsspråk kan vi tänka på det som ”både… och”. Inom programmering och digitalteknik används OCH-grindar för att styra flödet av information. En sanningstabell kan tydligt illustrera hur OCH-operationen fungerar:

A OCH B

Sann	Sann	Sann
Sann	Falsk	Falsk
Falsk	Sann	Falsk
Falsk	Falsk	Falsk

Denna operation är avgörande för att skapa komplexa logiska uttryck och används flitigt i villkorssatser inom programmering.

ELLER (Disjunktion)

ELLER-operationen, eller disjunktion, är sann om minst ett av de ingående påståendena är sanna. I vardagsspråk kan vi tänka på det som ”antingen… eller”. Inom digitalteknik används ELLER-grindar för att kombinera signaler. Även här kan en sanningstabell ge klarhet:

A ELLER B

Sann	Sann	Sann
Sann	Falsk	Sann
Falsk	Sann	Sann
Falsk	Falsk	Falsk

ELLER-operationen är central för att skapa flexibla logiska system som kan hantera olika scenarier.

ICKE (Negation)

ICKE-operationen, eller negation, inverterar ett påståendes sanningsvärde. Om ett påstående är sant, gör ICKE det falskt, och vice versa. I vardagsspråk kan vi tänka på det som ”inte”. Inom digitalteknik används ICKE-grindar för att invertera signaler. Sanningstabellen är enkel:

ICKE A

Sann	Falsk
Falsk	Sann

ICKE-operationen är grundläggande för att skapa logiska negationer och används i en mängd olika sammanhang.

Tillämpningar av Logiska Operationer

Logiska operationer är inte bara teoretiska koncept; de har praktiska tillämpningar inom många områden:

Programmering: Villkorssatser (if-satser) använder OCH, ELLER, och ICKE för att styra programflödet.
Digitalteknik: Logiska grindar (AND, OR, NOT) är byggstenarna i digitala kretsar.
Matematik: Boolesk algebra använder dessa operationer för att analysera och förenkla logiska uttryck.

Artificiell intelligens: Logiska operationer används i regelbaserade system och expertssystem.

Genom att förstå dessa operationer kan vi bättre analysera och lösa komplexa problem.

Slutsats

OCH, ELLOR, och ICKE är grundläggande logiska operationer som spelar en avgörande roll i många aspekter av vårt liv. Genom att behärska dessa operationer kan vi förbättra vårt logiska tänkande och lösa problem mer effektivt. Oavsett om du är en programmerare, matematiker eller bara en nyfiken tänkare, är kunskapen om dessa operationer ovärderlig.