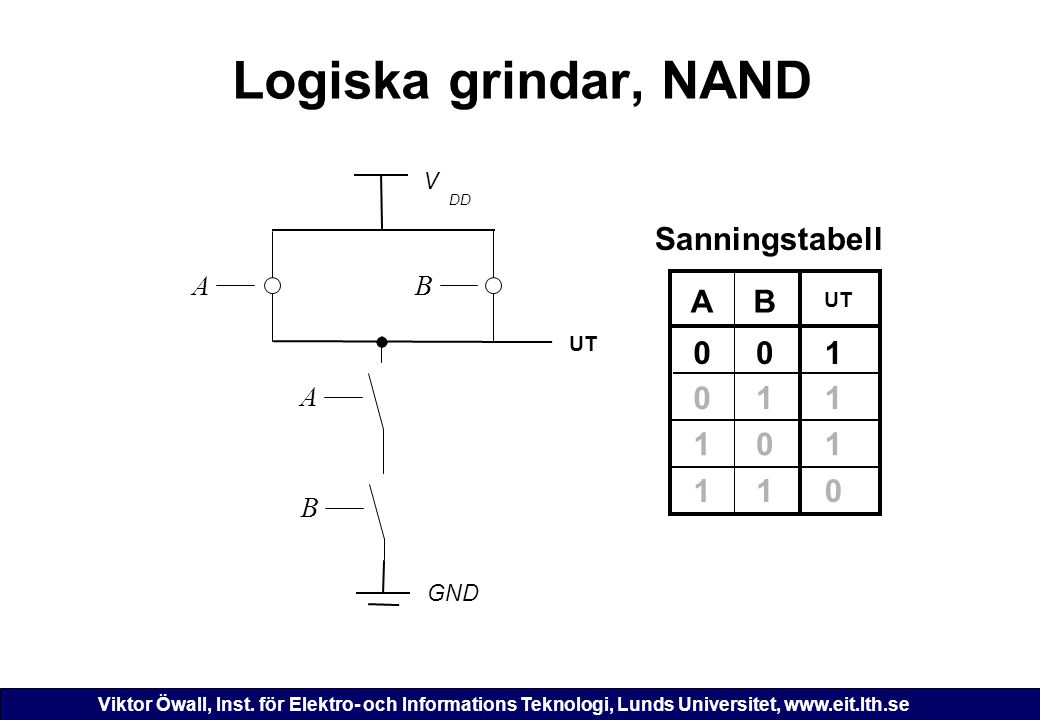
Sanningsvärdetabell (eller ofta bara sanningstabell, som är en direktöversättning av engelska truth table) är en teknik inom logiken utvecklad av Charles Peirce . Symboler, sanningstabeller och Booleska uttryck för grindar. En logisk funktion kan också beskrivas genom en sanningstabell (truth table).

I dessa lägen brukar man använda sanningstabeller för att kunna avgöra i vilka lägen ett uttryck är sant eller falskt. I en sådan tabell brukar man börja med de. Studera en grind i taget genom att koppla in den på det röda kopplingsbordet (ETS-7000) och fyll i sanningstabellerna nedan.
OR-krets; vi använder hädanefter de eng- elska namnen.

Figur 5b visar grindens sanningstabell och symbol, ”större än eller lika . Försök först själv skriva sanningstabellen för formeln. Visa med en sanningstabell, att , där A, B och C är tre satser med sanningsvärdena ett eller noll. Mata in dina logiska uttryck med variabler för att automatiskt skapa en sanningstabell.
Flera uttryck kan lätt jämföras, sida vid sida, i samma tabell. MaA- Satslogik (Sanningstabell och Tautologi). Vi kan göra en sanningstabell för att avgöra sanningshalten hos de kombinerade påståendena. Först skriver vi de olika satserna och sist skriver vi det .

.jpg&ehk=MXE3aMuiJoHilKIjsqlgnpzR21cgCKIKPDG8rnYDPsc%3d&risl=&pid=ImgRaw&r=0)