lika långa

Hur Manga Symmetrilinjer Har En Rektangel

av

Hur många symmetrilinjer har en rektangel?

När vi talar om geometriska former, är symmetri ett viktigt begrepp. Men hur många symmetrilinjer har egentligen en rektangel? Låt oss utforska detta i detalj.

Vad är en symmetrilinje?

Hur Manga Symmetrilinjer Har En Rektangel

En symmetrilinje, eller symmetriaxel, är en linje som delar en figur i två exakt likadana halvor. Om du skulle vika figuren längs denna linje, skulle de två halvorna passa perfekt ovanpå varandra. Detta kallas spegelsymmetri eller linjesymmetri.

Hur Manga Symmetrilinjer Har En Rektangel

Rektangelns egenskaper

En rektangel är en fyrhörning med fyra räta vinklar. Den har två par av parallella sidor, där de motstående sidorna är lika långa. Dessa egenskaper påverkar direkt antalet symmetrilinjer.

Antalet symmetrilinjer i en rektangel

En rektangel har exakt två symmetrilinjer. Dessa linjer går genom mittpunkterna på de motstående sidorna. En linje går horisontellt, och den andra går vertikalt.

Hur Manga Symmetrilinjer Har En Rektangel
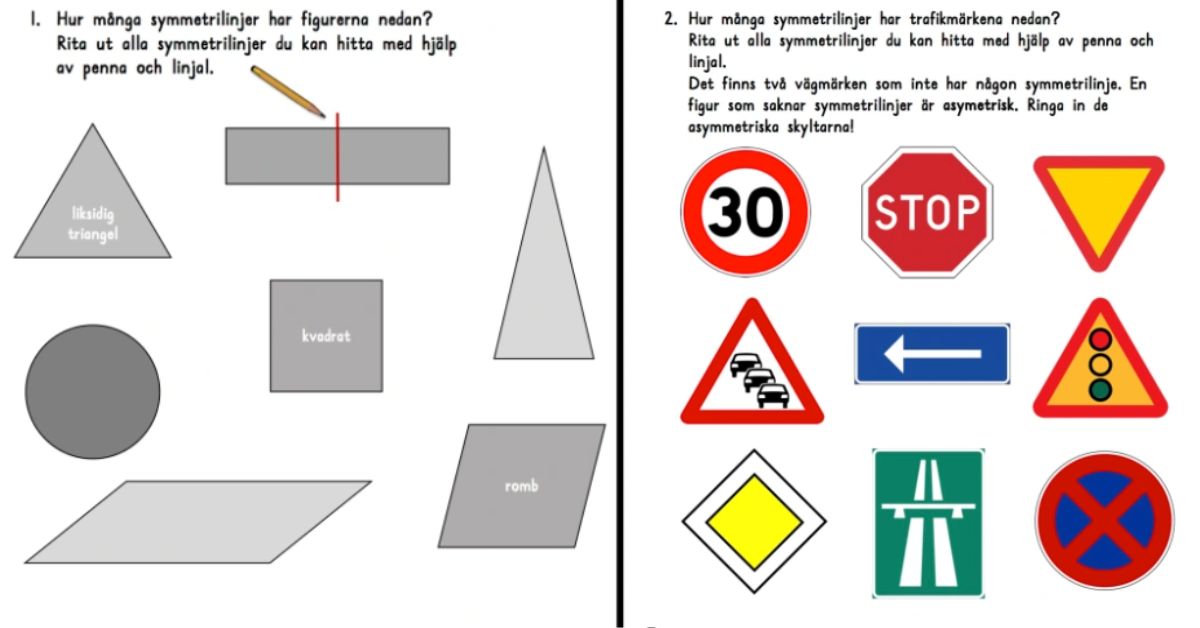
  1. Horisontell symmetrilinje: Denna linje delar rektangeln i två lika stora horisontella halvor.
  2. Vertikal symmetrilinje: Denna linje delar rektangeln i två lika stora vertikala halvor.
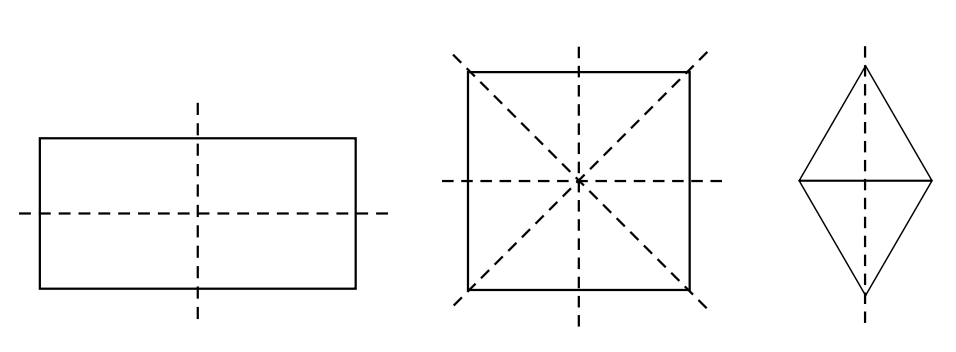
    3. Hur Manga Symmetrilinjer Har En Rektangel
Hur Manga Symmetrilinjer Har En Rektangel

Det är viktigt att notera att diagonalerna i en rektangel inte är symmetrilinjer, såvida rektangeln inte är en kvadrat. En kvadrat är en speciell typ av rektangel där alla sidor är lika långa, och den har fyra symmetrilinjer.

Visuell förklaring

Hur Manga Symmetrilinjer Har En Rektangel

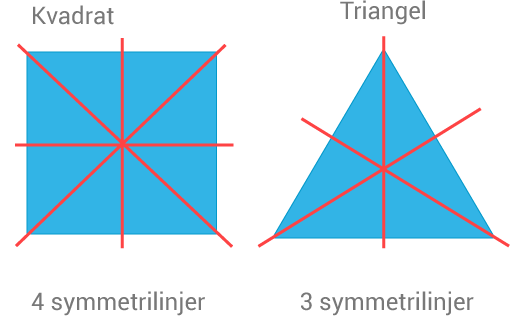
Tänk dig en rektangel på ett papper. Om du viker papperet exakt på mitten längs den horisontella linjen, kommer de två halvorna att passa perfekt ovanpå varandra. Samma sak gäller om du viker längs den vertikala linjen.

Denna visuella representation hjälper till att förstå hur symmetrilinjerna fungerar i en rektangel.

Varför är detta viktigt?

Att förstå symmetrilinjer är grundläggande inom geometri och matematik. Det hjälper oss att analysera och kategorisera former. Dessutom har symmetri tillämpningar inom konst, design och arkitektur.

Sammanfattning

En rektangel har två symmetrilinjer: en horisontell och en vertikal. Dessa linjer delar rektangeln i två exakt likadana halvor. För att förstå symmetri fullt ut, är det viktigt att känna till de grundläggande egenskaperna hos geometriska former.

Vanliga frågor

  • Har en kvadrat fler symmetrilinjer än en rektangel? Ja, en kvadrat har fyra symmetrilinjer eftersom den har lika långa sidor.
  • Är diagonalerna symmetrilinjer i en rektangel? Nej, inte om rektangeln inte är en kvadrat.
  • Varför är symmetri viktigt inom geometri? Symmetri hjälper oss att förstå och klassificera former.

Vi hoppas att denna artikel har gett dig en klar förståelse för antalet symmetrilinjer i en rektangel. Fortsätt att utforska geometrins fascinerande värld!

Optical Illusions

av

Optiska Illusioner: En Fascinerande Värld av Synbedrägerier

Optical Illusions

Har du någonsin sett en bild som verkar röra sig, trots att den är helt stilla? Eller en linje som ser längre ut än en annan, fast de är lika långa? Då har du upplevt en optisk illusion! Optiska illusioner är verkligen häpnadsväckande och visar hur våra ögon och hjärnor kan luras. I den här artikeln ska vi utforska denna fascinerande värld och lära oss mer om hur de fungerar.

Vad är Optiska Illusioner?

En optisk illusion, eller synvilla, är en visuell upplevelse där det vi ser inte stämmer överens med den faktiska verkligheten. Det beror på hur våra ögon och hjärnor tolkar informationen de får. Vår hjärna försöker skapa mening av det vi ser, och ibland gör den det på ett sätt som inte är helt korrekt. Detta kan bero på olika faktorer, som ljus, färger, former och perspektiv.

Optical Illusions

Kända Optiska Illusioner

Müllers Illusion

Optical Illusions

Müllers illusion är en klassisk illusion där två linjer med pilar i ändarna ser olika långa ut, trots att de är lika långa. Pilarna som pekar inåt gör att linjen ser kortare ut, medan pilarna som pekar utåt gör att linjen ser längre ut. Det är ett perfekt exempel på hur perspektiv kan lura oss.

Ames Rum

Ames rum är en annan berömd illusion som skapar en förvrängd uppfattning av storlek. Rummet är konstruerat så att det ser rektangulärt ut från ett visst perspektiv, men i verkligheten är det trapetsformat. Det gör att personer som rör sig i rummet verkar krympa eller växa.

Den Rörliga Cirkeln

Det finns många bilder som ser ut att röra sig fast de är statiska. Dessa illusioner använder sig av mönster och färger för att skapa en känsla av rörelse. När du tittar på dessa bilder, kan du känna att ditt sinne blir förvirrat.

Hur Fungerar Optiska Illusioner?

Optiska illusioner fungerar genom att utnyttja hur vår hjärna tolkar visuell information. Vår hjärna försöker fylla i luckor och skapa en sammanhängande bild av världen. Ibland använder den sig av genvägar och antaganden som inte är helt korrekta. Det kan bero på:

    Optical Illusions
  • Kontraster: Hur ljus och mörk påverkar vår uppfattning.
  • Färger: Hur olika färger interagerar med varandra.
  • Perspektiv: Hur avstånd och vinklar påverkar vår syn.
    • Optical Illusions
  • Mönster: Hur upprepade mönster kan lura vår hjärna.
Optical Illusions

Genom att förstå dessa principer kan vi bättre förstå varför vi ser optiska illusioner.

Varför Är Optiska Illusioner Intressanta?

Optiska illusioner är inte bara roliga och underhållande, de är också viktiga inom vetenskap och psykologi. De hjälper oss att förstå hur vår hjärna fungerar och hur vi uppfattar världen omkring oss. Genom att studera illusioner kan forskare lära sig mer om syn, perception och kognition.

Dessutom är de ett fantastiskt sätt att utmana vår uppfattning av verkligheten och öppna upp för nya perspektiv.

Slutsats

Optiska illusioner är en otrolig del av vår visuella upplevelse. De visar hur komplex och ibland felbar vår hjärna kan vara. Nästa gång du ser en optisk illusion, ta dig tid att fundera över hur den fungerar och vad den säger om hur vi uppfattar världen.